Problems tagged with "computing loss"

Consider the data set shown below. The ``\(\times\)'' points have label +1, while the ``o'' points have label -1. Shown are the places where a linear prediction function \(H\) is equal to zero, 1, and -1.

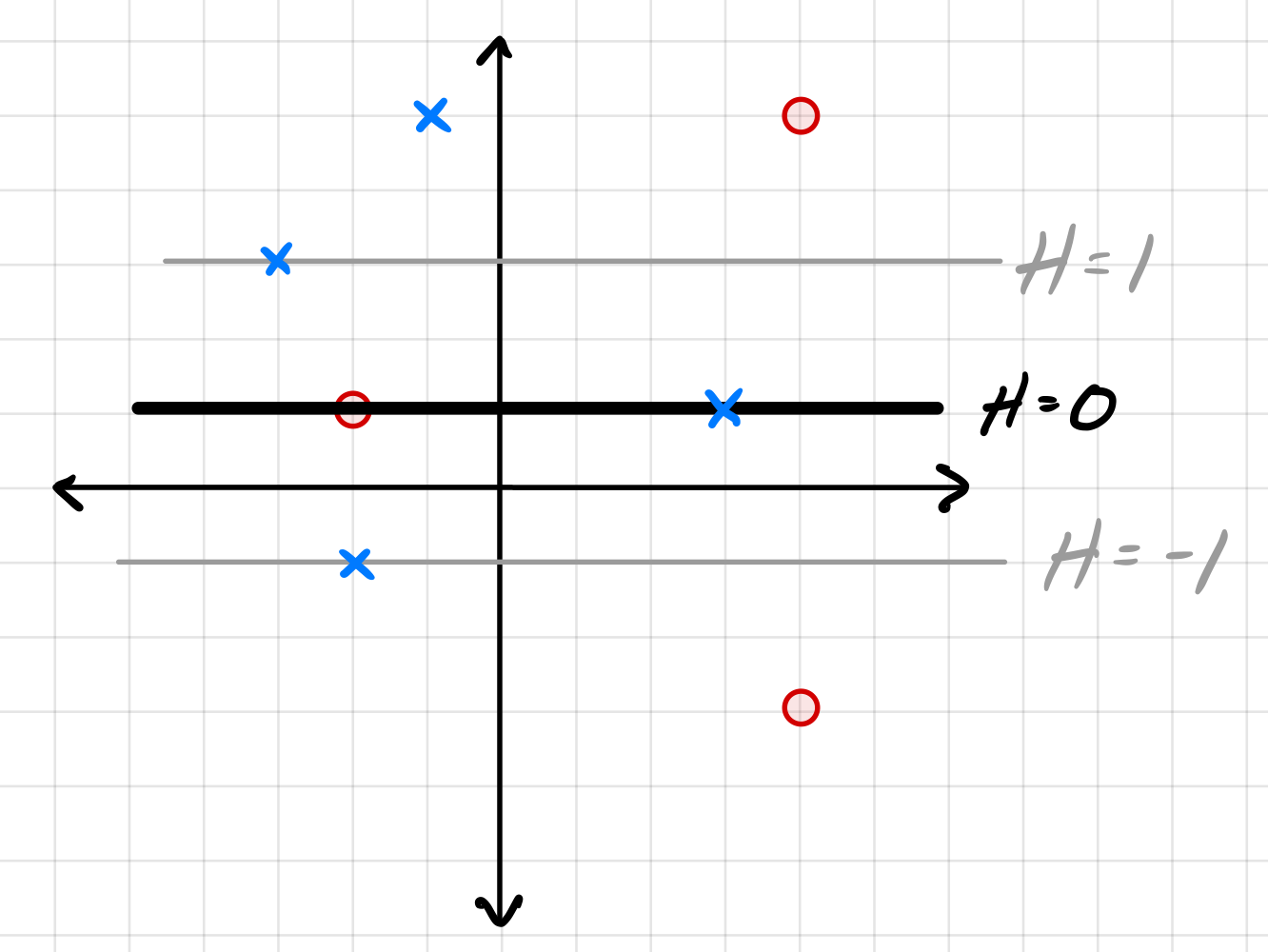
For each of the below subproblems, calculate the total loss with respect to the given loss function. That is, you should calculate \(\sum_{i=1}^n L(\nvec{x}{i}, y_i, \vec w)\) using the appropriate loss function in place of \(L\). Note that we have most often calculated the mean loss, but here we calculate the total so that we encounter fewer fractions.

Consider the data set shown below. The ``\(\times\)'' points have label -1, while the ``\(\circ\)'' points have label +1. Shown are the places where a linear prediction function \(H\) is equal to zero (the thick solid line), 1, and -1 (the dotted lines). Each cell of the grid is 1 unit by 1 unit.

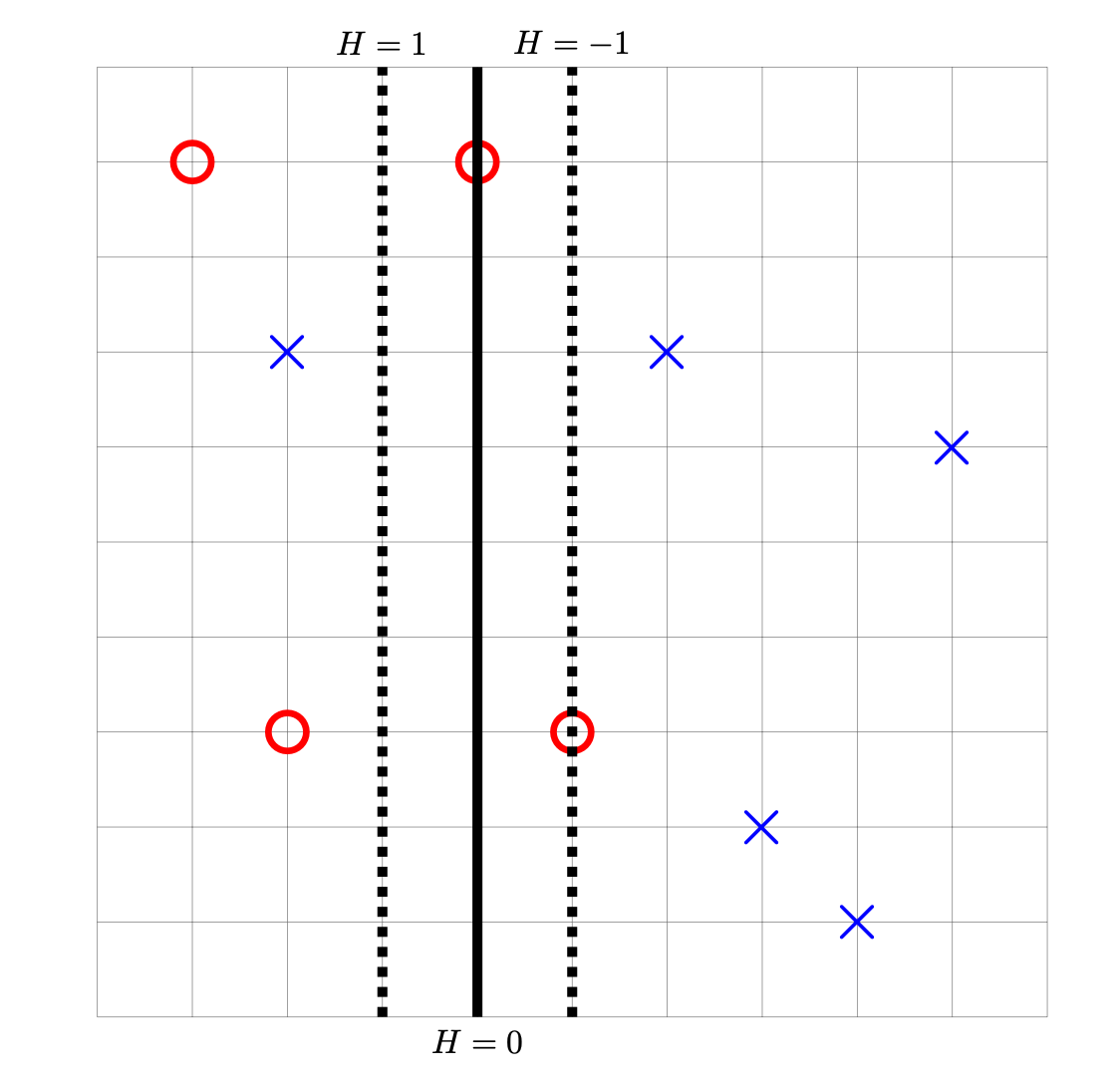
For each of the below subproblems, calculate the total loss with respect to the given loss function. That is, you should calculate \(\sum_{i=1}^n L(\nvec{x}{i}, y_i, \vec w)\) using the appropriate loss function in place of \(L\). Note that we have most often calculated the mean loss, but here we calculate the total so that we encounter fewer fractions.

Consider the data set shown below. The 4 points marked with ``+'' have label +1, while the 3 ``\(\circ\)'' points have label -1. Shown are the places where a linear prediction function \(H\) is equal to zero (the thick solid line), 1, and -1 (the dotted lines). Each cell of the grid is 1 unit by 1 unit. The origin is not specified; it is not necessary to know the absolute coordinates of the data to complete this problem.

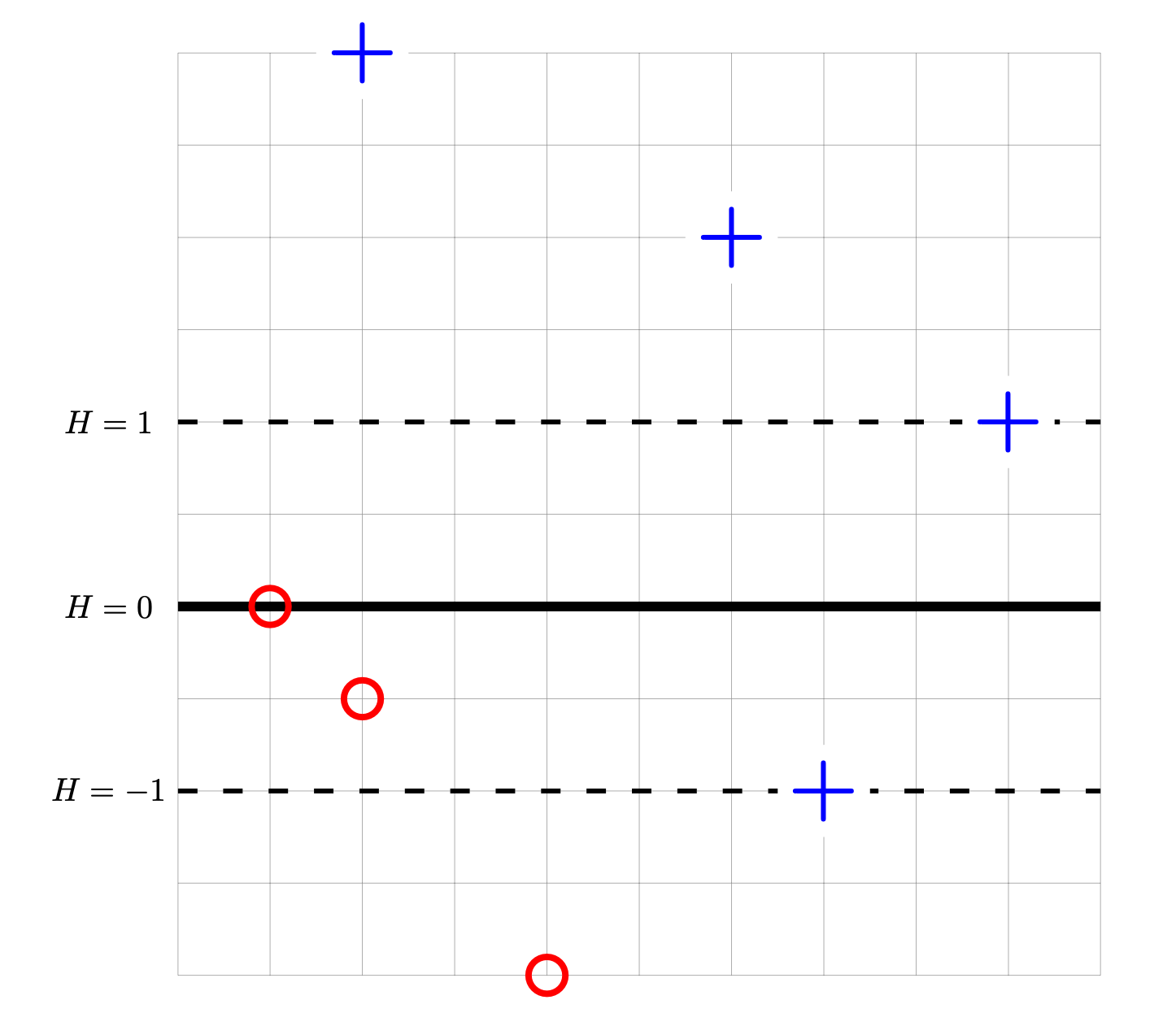
For each of the below subproblems, calculate the total loss with respect to the given loss function. That is, you should calculate \(\sum_{i=1}^n L(\nvec{x}{i}, y_i, \vec w)\) using the appropriate loss function in place of \(L\). Note that we have most often calculated the mean loss, but here we calculate the total so that we encounter fewer fractions.

Consider the data set shown below. The \(\diamond\) points marked with ``+'' have label +1, while the \(\circ\) points marked with ``\(-\)'' have label -1. Shown are the places where a linear prediction function \(H\) is equal to zero (the thick solid line), 1, and -1 (the dotted lines). Each cell of the grid is 1 unit by 1 unit. The origin is not specified; it is not necessary to know the absolute coordinates of the data to complete this problem.

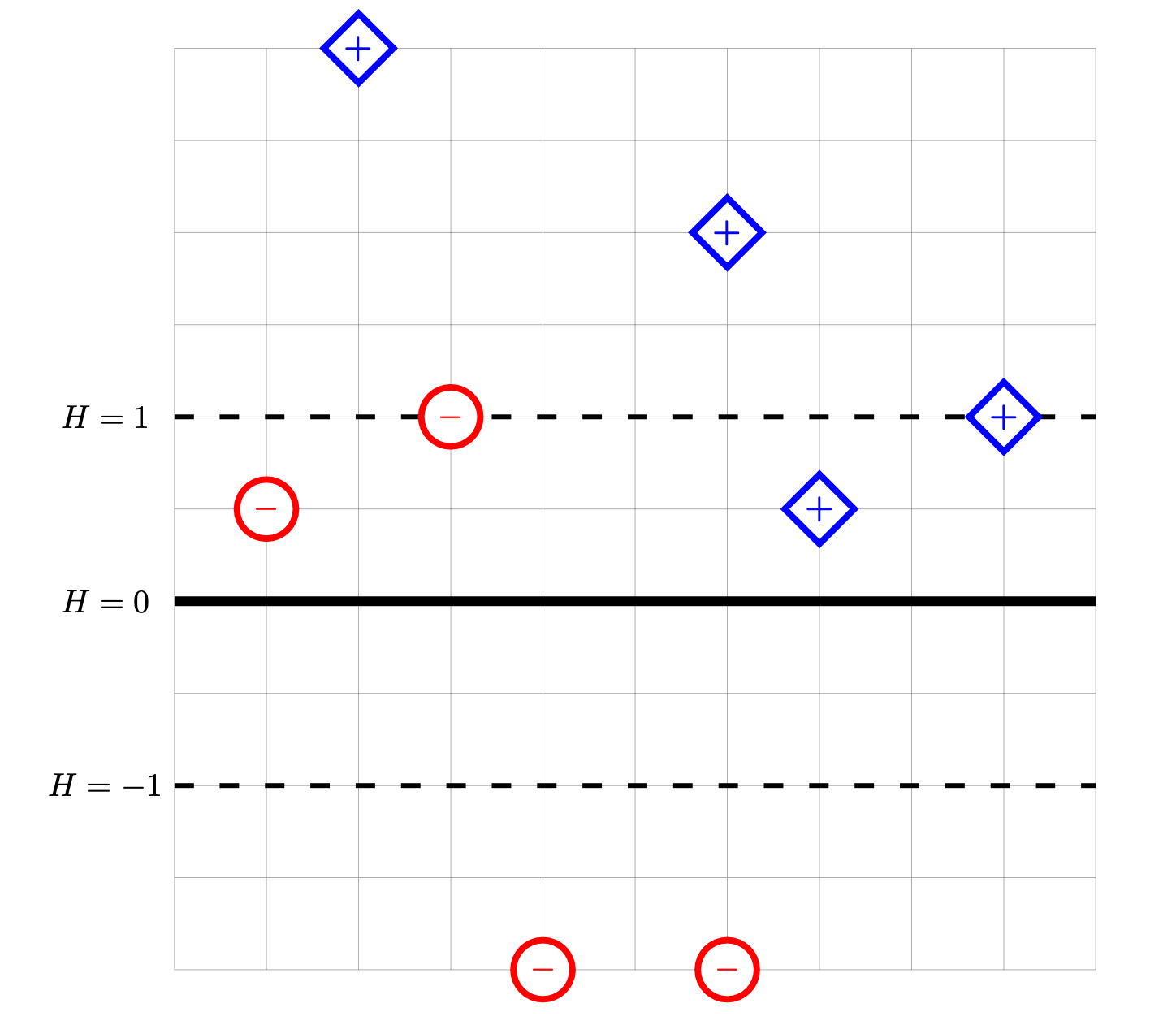
For each of the below subproblems, calculate the total loss with respect to the given loss function. That is, you should calculate \(\sum_{i=1}^n L(\nvec{x}{i}, y_i, \vec w)\) using the appropriate loss function in place of \(L\). Note that we have most often calculated the mean loss, but here we calculate the total so that we encounter fewer fractions.

Note: please double-check your calculations! We are not grading your work, so partial credit is difficult to assign on this problem.